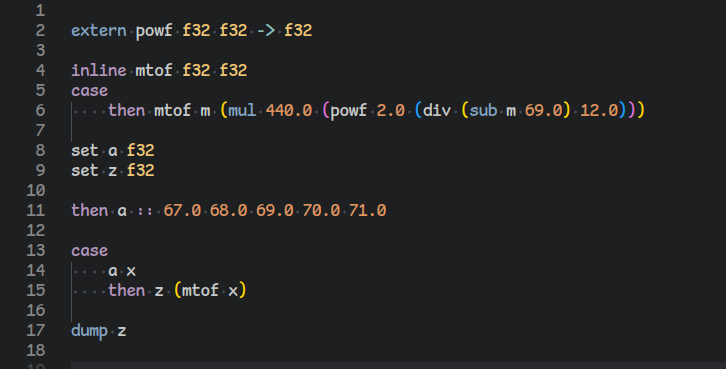
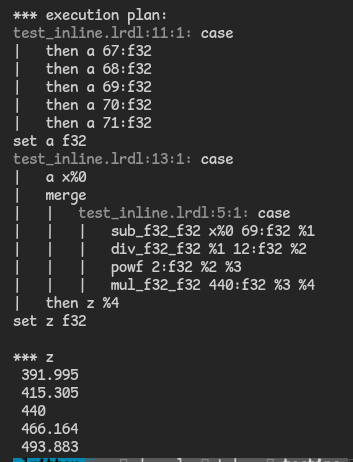
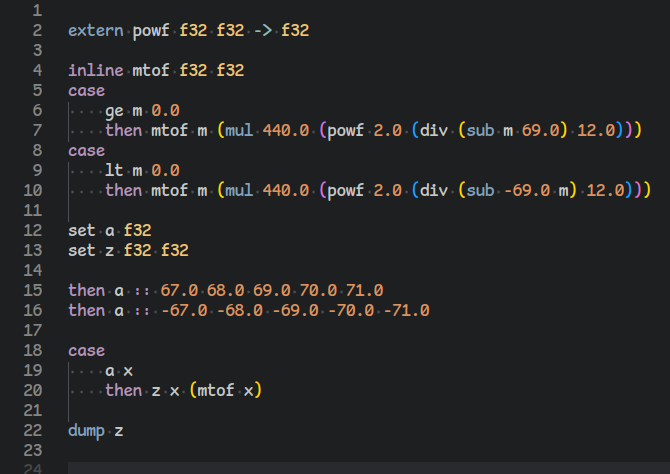
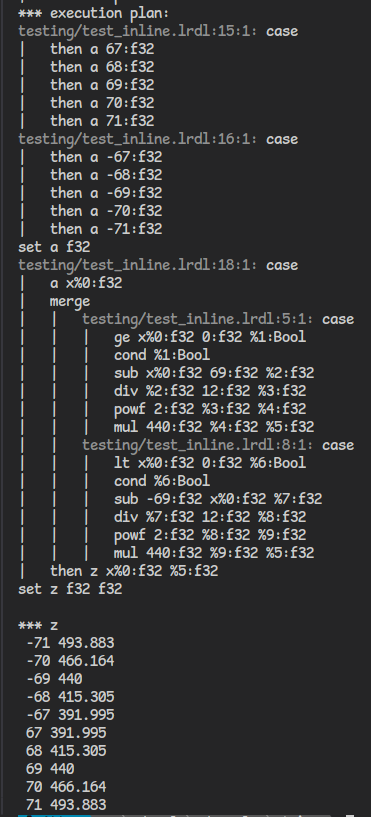
Today's changes include the addition of screen space reflections, which can be disabled via the settings.json file. There is also a more detailed cockpit and a bug that caused the game to crash when motion blur was disabled has been fixed.
https://codeberg.org/wesfly/bevy-fs
#rust #rustlang #gamedev #FlightSim #aviation #bevy #helicopter #airplane #DevLog