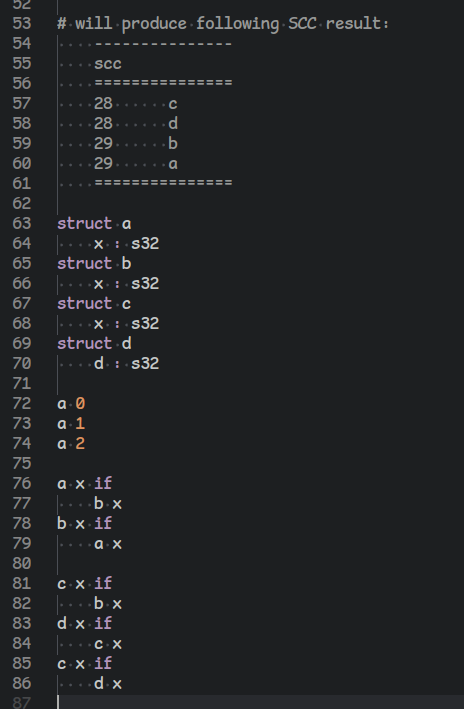
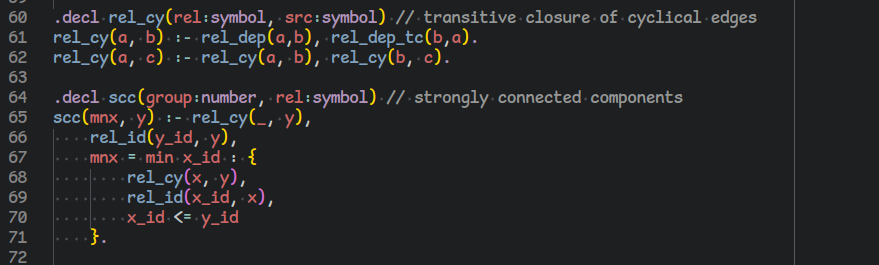
with a few more lines, we can extract the strongly connected components of the dependency graph (answering which vertices belong in the same loop). the work done is so far easily equivalent to 200 lines of C++.
Discussion
with a few more lines, we can extract the strongly connected components of the dependency graph (answering which vertices belong in the same loop). the work done is so far easily equivalent to 200 lines of C++.


this single rule discovers all direct edges between relational tables; it looks at every rule, gets its conclusion relation, then goes through all connected premises, and retrieves the relation from each premise.
all right-hand side terms are commutative, so you can read them in any order. together, they form a product (or an AND combination): when one term yields no results, then the entire outcome fails.
bonus relation: transitive closure.
with a few more lines, we can extract the strongly connected components of the dependency graph (answering which vertices belong in the same loop). the work done is so far easily equivalent to 200 lines of C++.


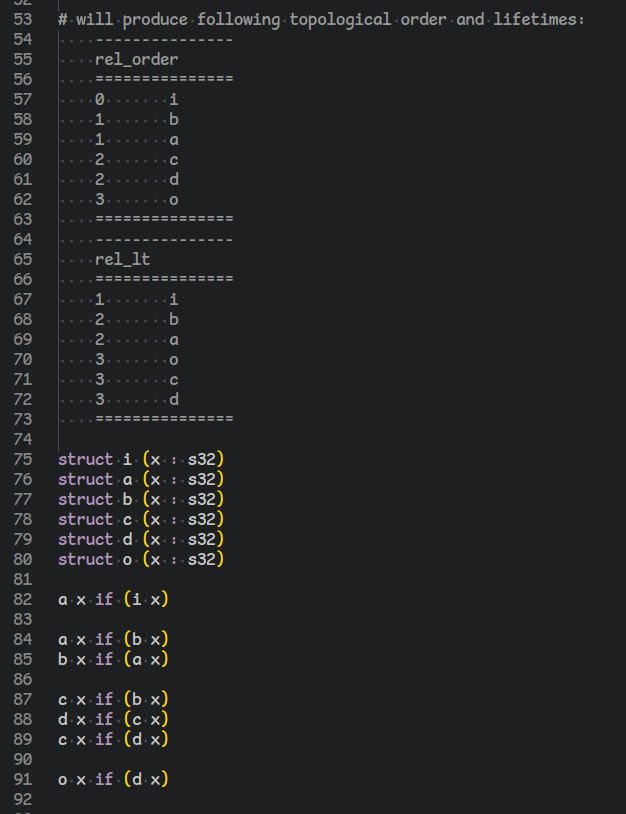
and then finally, with all information we have extracted, we can toposort the SCC graph, and that's our stratified execution schedule for the program.
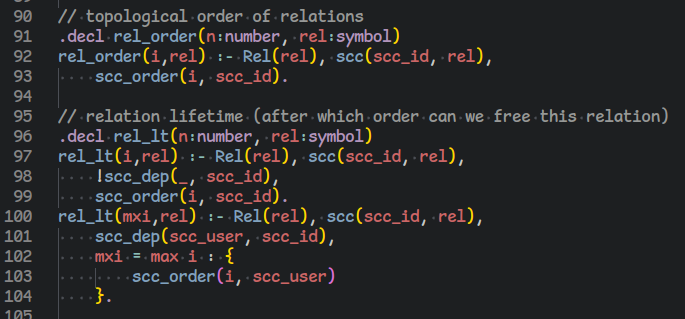
the next interesting question to ask, with the information we have, is: when can we release which resource?
and the answer to our lifetime problem are these two rules. now we have, in addition to the execution order of our program, the release order of our resources.
A space for Bonfire maintainers and contributors to communicate