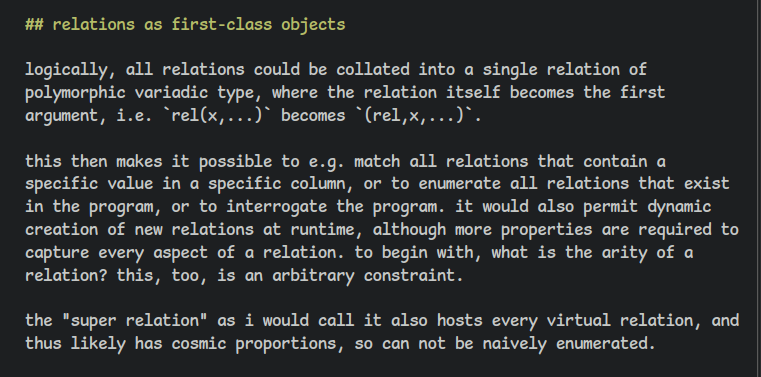
pretty proud of what i wrote but also feeling i just made the job harder for myself... BUT IMAGINE THE POWER
Discussion
Loading...
Discussion
also this. also probably best for an interpreter, because a compiler would require significant preprocessing and analysis to make it fast.
i forgot to add that it also permits to use relations as arguments, so you can remap relations and build lookup tables, use them like closures, and all that jazz.
@lritter cant wait to read a comprehensive book about it 🙂
bonfire.cafe
A space for Bonfire maintainers and contributors to communicate
Automatic federation enabled