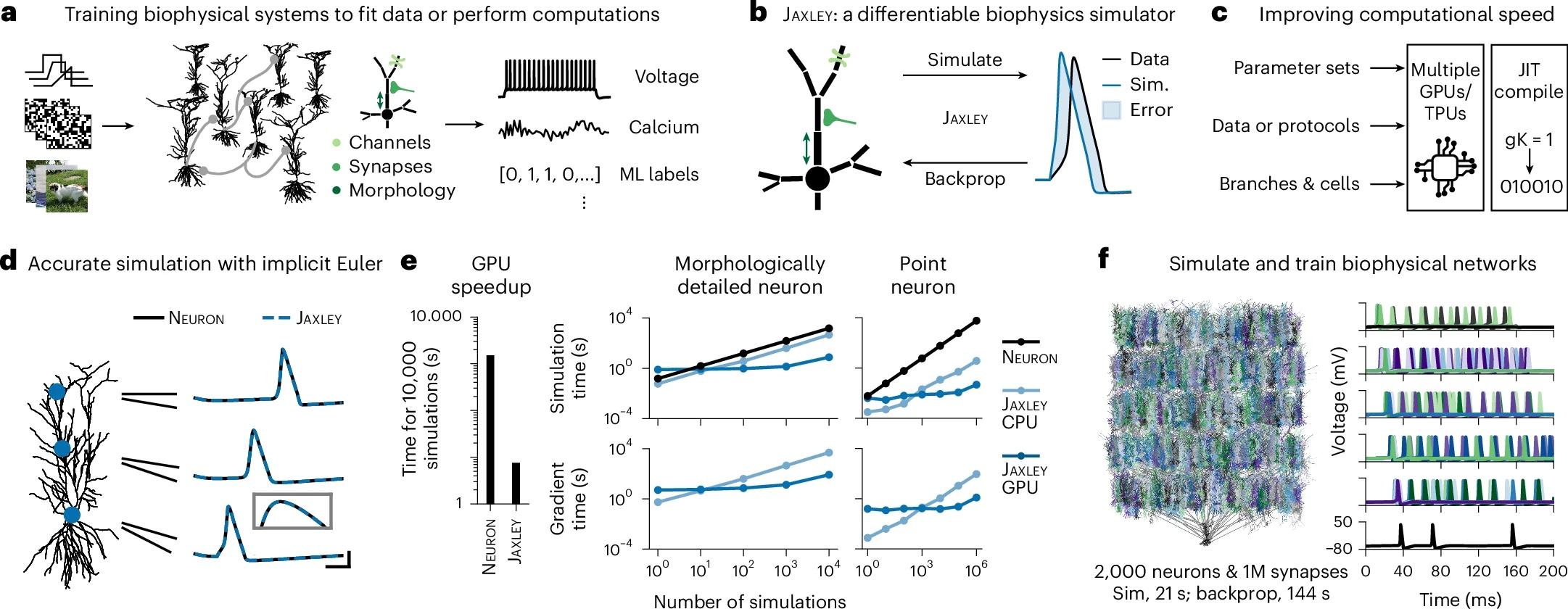
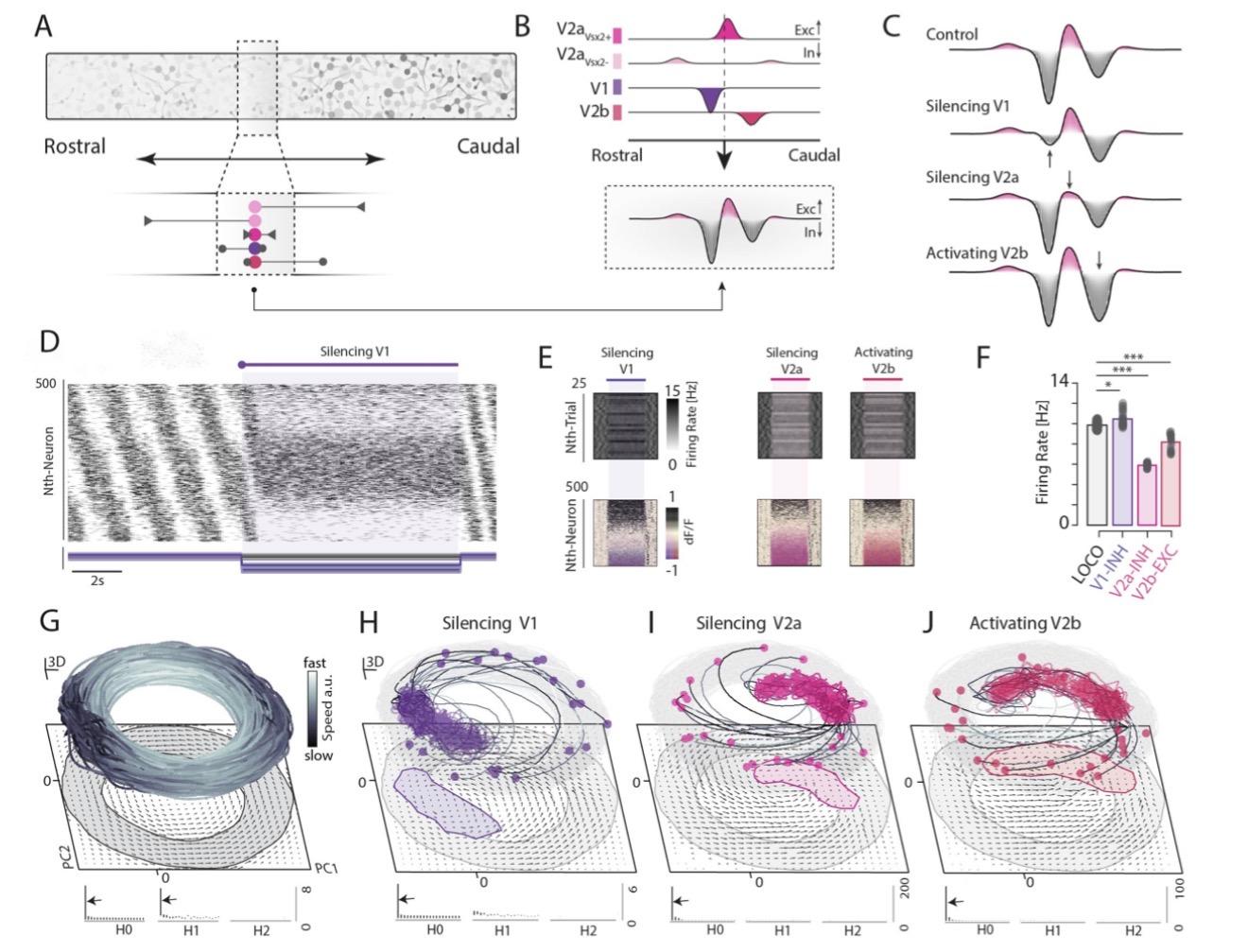
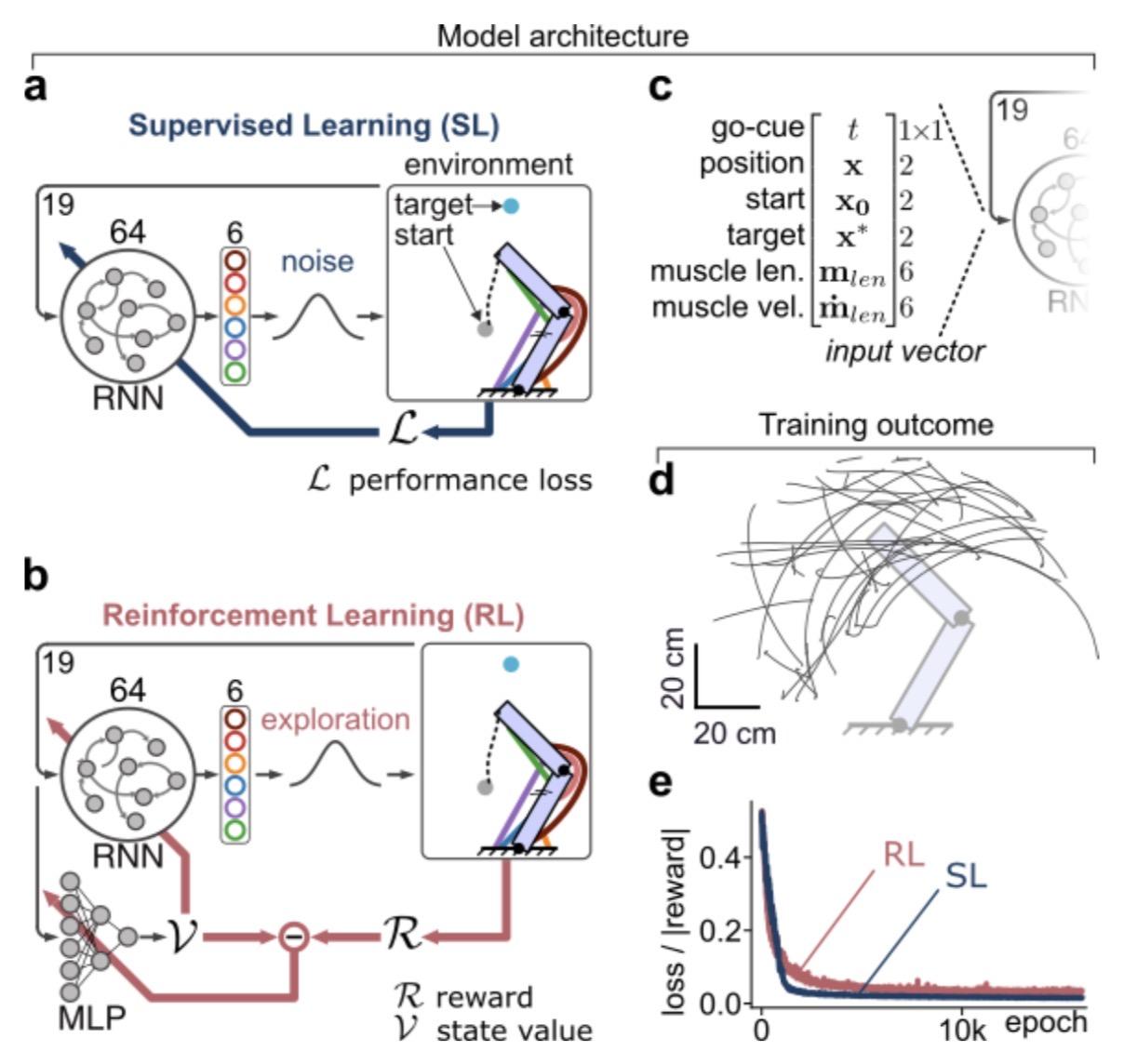
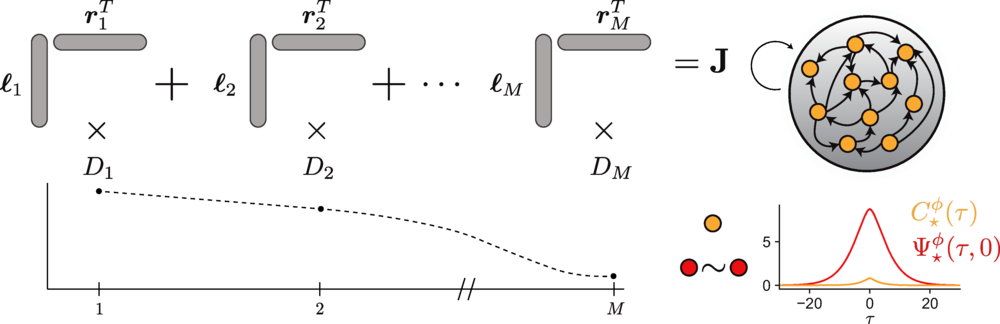
🧠 New preprint by Shervani-Tabar, Brincat & @ekmiller on emergent #TravelingWaves in #RNN.
By aligning RNN dynamics to an empirically measured #NeuralManifold, they show that task-relevant TW can emerge through #learning, w/o hard-coding wave dynamics or connectivity. The cool thing here is that the waves are not imposed or engineered, but emerge naturally from learning under #BiologicallyPlausible constraints: