I can't believe I didn't know this fact before today - it seems so fundamental.

If you have a real symmetric matrix A, and pick some unit vector x, then it's standard textbook material that x.Ax (the Rayleigh quotient) is bounded by the smallest and largest eigenvalues. So what happens if I pick a random unit vector, how is x.Ax distributed?

Let's jump to the case of a Hermitian matrix A and a random unit vector on the complex sphere. How is T=conj(x).A.x distributed? Again it's standard that it's bounded between the smallest and largest eigenvalue.

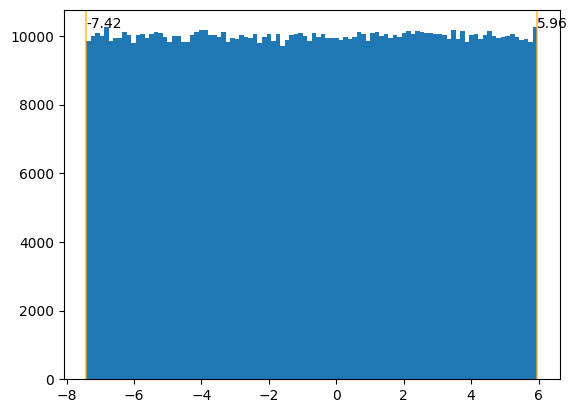
We can start with a 2x2 matrix A. First surprise to me: T is distributed *uniformly* between the two eigenvalues.

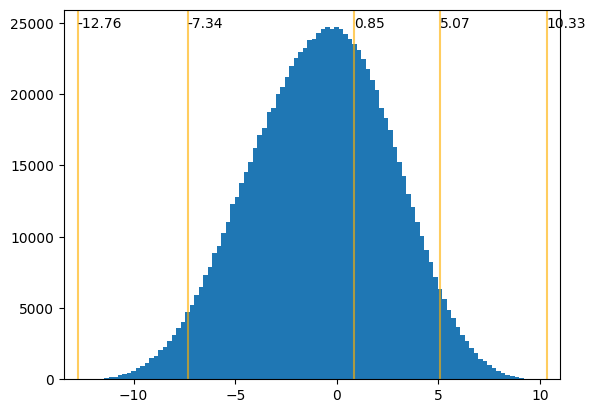
The first plot below is the histogram of values of T for 1,000,000 vectors x and a randomly chosen Hermitian matrix A. The yellow lines mark the two eigenvalues.

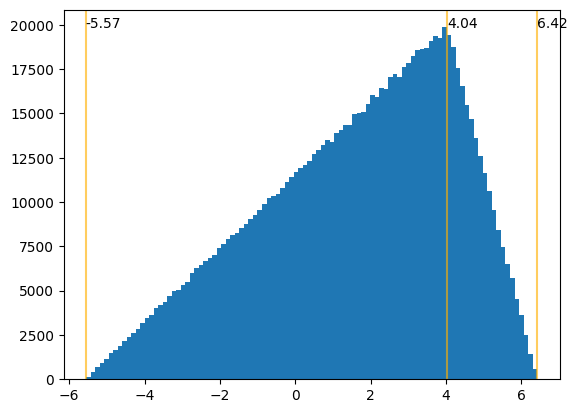
Now try 3x3. Remarkably the distribution is piecewise linear with the break points at the eigenvalues.

And let's jump to 5x5. We get the third plot, whose curve is given by a cubic B-spline with control points given by the eigenvalues.

Bizarrely you can prove you always get B-splines making this one of the few times I've seen B-splines in "nature", so to speak.

This is a purely mathematical result but I found it in this paper on wave transport through random media: https://arxiv.org/abs/2511.04602

My calculations (pretty much the same as the paper) are here: https://colab.research.google.com/drive/1g7ImBblYAsninp5-sr6uWQTVfTYurerE?usp=sharing