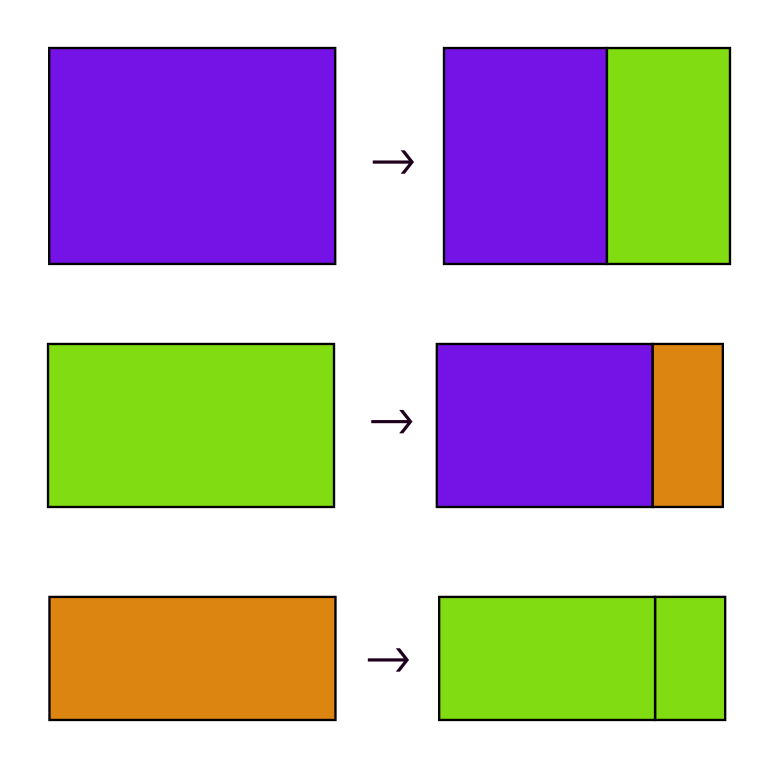
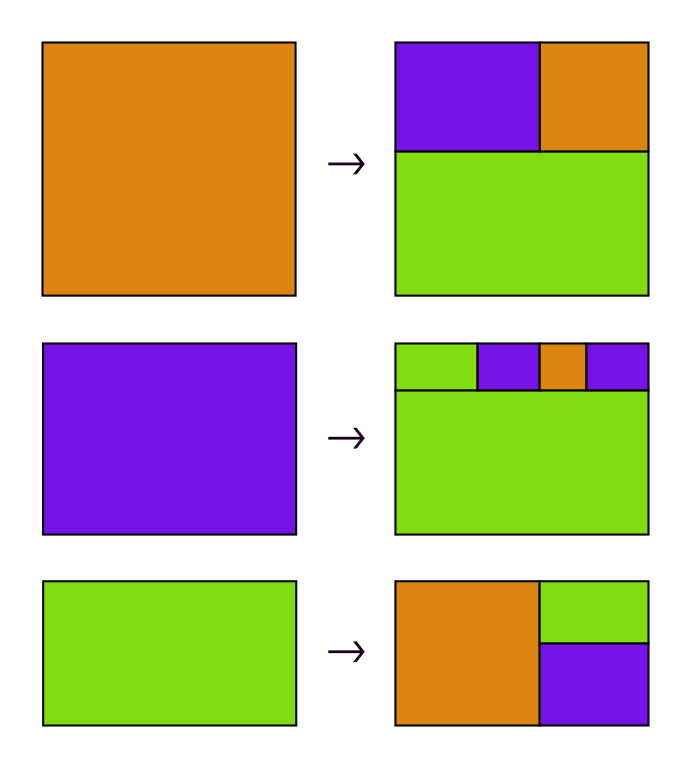
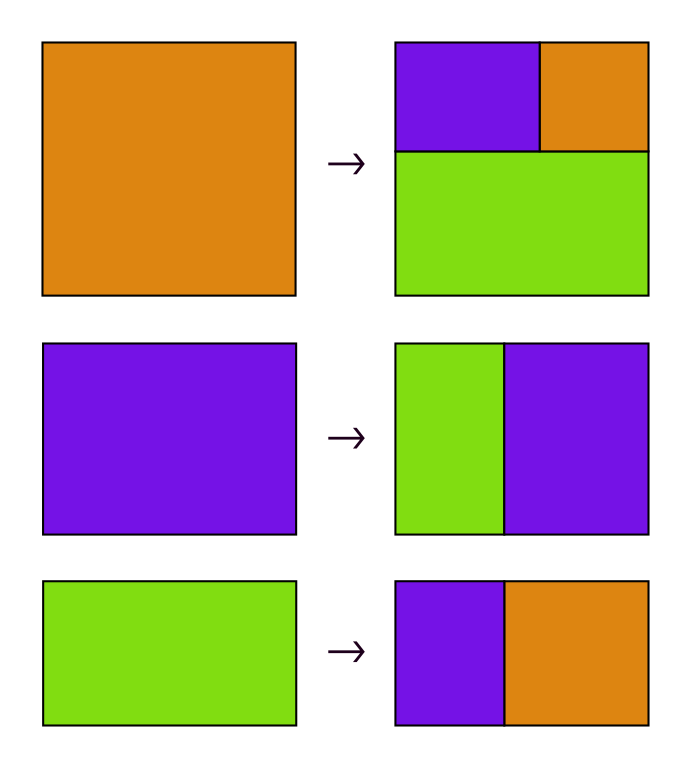
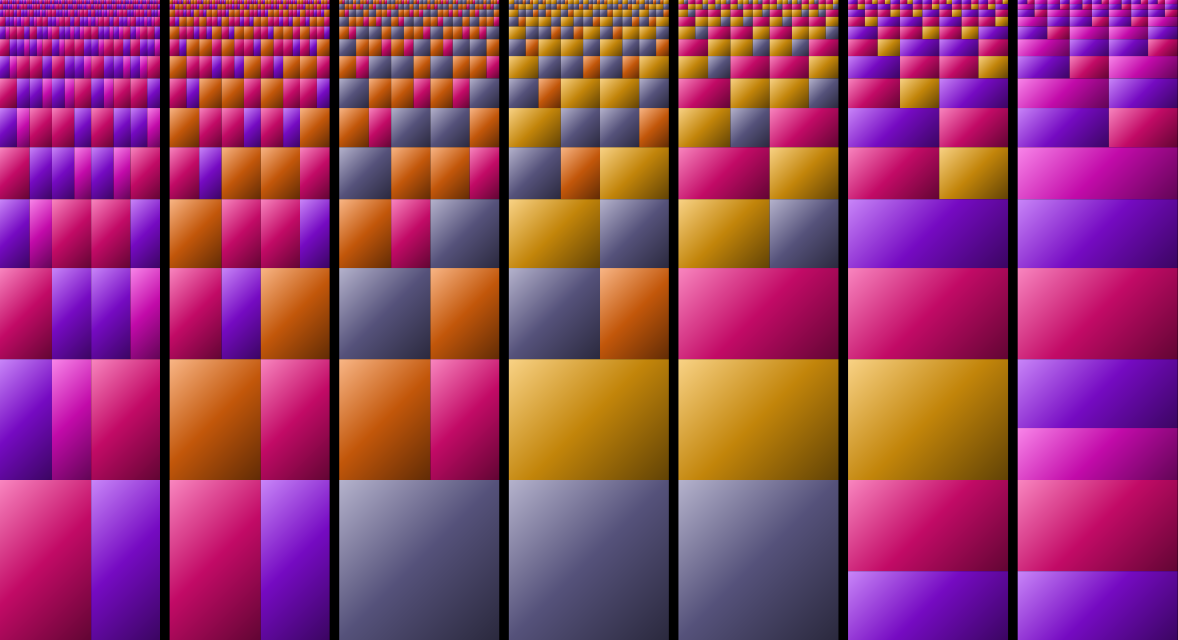
[1/n] Continuing my work (see previous posts) about the geometric possibilities of the radiant number ρ (aka plastic ratio). Because it can serve as the base of a numeral system (just it and the golden ratio have this property among non-integers), every rectangle whose side ratio is a power of ρ can be decomposed into rectangles whose side ratio is a power of ρ. Particularly, if we take three consecutive powers of ρ we can make substitution tilings involving its corresponding rectangles. These properties are depicted in the first image. In the next images we see two possibilities regarding rectangles of ratios 1, ρ and ρ² (one just uses horizontal rectangles), and one for rectangles of ratios ρ, ρ² and ρ³. Of course any of these partitions, by rearranging/rotating/mirroring tiles, give many possible different tilings.
#Mathematics #geometry #tiling #mathart #radiantnumber