Cirno's Math Class : SOL Calibration for Dummies #electronics

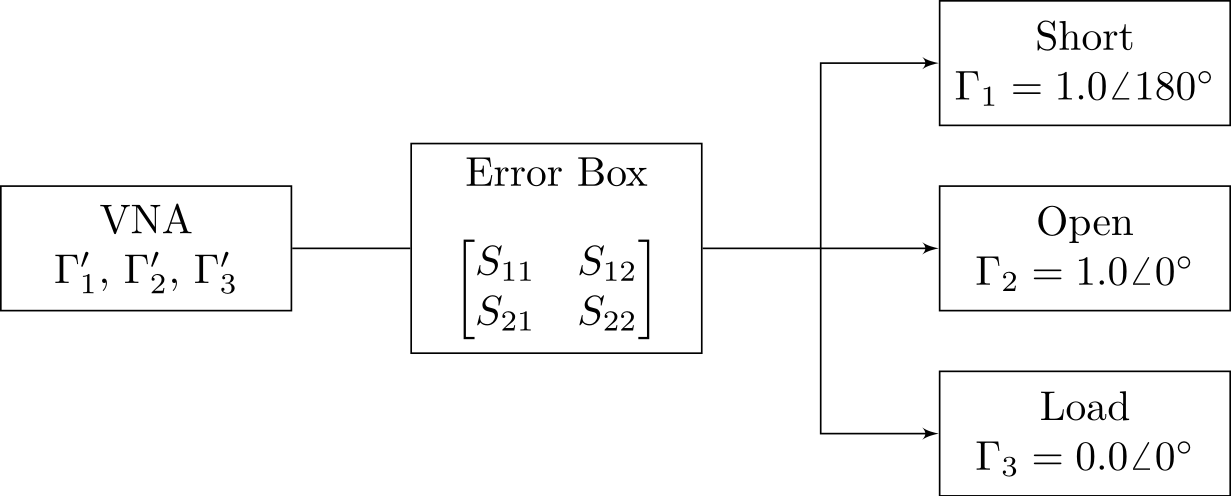
In one-port measurements, a VNA's measurement readings contain linear errors. One can represent the Device-Under-Test (DUT) as a cascade of an irremovable two-port error network (Error Box) and the true DUT. The true reflection coefficient Γ is modified by Error Box into the imperfect reading Γ′.

The Error Box represents both the signal path errors (e.g. mismatch reflection, electrical delay/phase shift) and VNA's internal receiver errors. Like all two-port networks, one can define it using 4 S-parameters: S₁₁, S₂₁, S₁₂ and S₂₂.

Using the standard formula to cascade a 2-port and a 1-port network, we find the measured reflection coefficient is:

Γ′ = [S₁₁ − (S₁₁S₂₂ − S₂₁S₁₂)Γ] / (1 − S₂₂Γ)

All four S-parameters of the Error Box are mixed with the DUT's reflection coefficient Γ, including a difficult cross-term (S₁₁S₂₂ − S₂₁S₁₂) - apparently making them unsolvable. But we only care about the overall error, not individual terms. Thus we can linearize the equations as such:

m₁ = 1 x₁ = S₁₁
m₂ = ΓΓ′ x₂ = S₂₂
m₃ = −Γ x₃ = S₁₁S₂₂ − S₂₁S₁₂

The left-hand side is fully known, because they only contain known measurement reading Γ′, and the DUT's true reflection coefficient Γ - which is known when for characterized calibration kits.

Notably, there are only 3 out of 4 variables left. Intuitively, it means that both the forward (Port 1 to Port 2) and reverse path (Port 2 to Port 1) in the Error Box can attenuate a signal. They're indistinguishable by one-port measurements alone, so there are three effective error terms only. Some papers assume reciprocity (S₁₂ = S₂₁) or explicitly normalize one variable away (S₂₁ = 1).

Substitute the variables in the original equations, we obtain a linear equation:

Γ′ = (x₁ − x₃Γ) / (1 − x₂Γ)
Γ′ − ΓΓ′x₂ = x₁ − Γx₃
Γ′ − m₂x₂ = m₁x₁ + m₃x₃
Γ′ = m₁x₁ + m₂x₂ + m₃x₃

When we have three calibration standards with arbitrary reflection coefficients Γ₁, Γ₂, Γ₃, and three imperfect measurement readings Γ₁′, Γ₂′, Γ₃′ (such as Short, Open, Load). We have a linear system of equations with three unknowns, a standard high-school math question.

m₁₁x₁ + m₁₂x₂ + m₁₃x₃ = Γ₁′
m₂₁x₁ + m₂₂x₂ + m₂₃x₃ = Γ₂′
m₃₁x₁ + m₃₂x₂ + m₃₃x₃ = Γ₃′

Once solved, x₁, x₂ and x₃ can be plugged into the first equation to find the perfect Γ from Γ′ for all future measurements.

Note how Γ₁, Γ₂, Γ₃ need not to be perfect, just be known. This only practical requirement is that they must maintain a distance from each other on the complex plane. If two measurements are too close, the system is ill-conditioned since an equation has been lost. Short and Open are common choices because they are always 180° away ideally.